駒田 寛 のサイト
FDTD法計算について書きました
私がFDTD法と出会ったのは2009年に九州大学でテクニカルスタッフとして勤務していた時でした。マイクロ・ミリ波の伝搬をシミュレーションをするプログラムを上司である教授からもらいました。始めてみたときは驚きました。10年以上も前に学生として電気電子工学を勉強して、その時に電磁気学の授業でマクスウェル方程式(電磁気学の基礎方程式)というものをならって、それから結構な時間、演習問題を解いてきて、結局よくわからなかったものが、(Yeeアルゴリズムの部分だけだと)たった2ページぐらいに収まるソースプログラムの実行結果だったというのです。それから、いろいろあったわけですが、まずは以下の圧縮済みフォルダをダウンロードしてから解凍してみてください。
解凍したフォルダー「FolderA」の中身
1. FORTRANファイル「FDTD3dp01.f」(ブラウザ表示用)
2. FORTRANファイル「FDTD3dm7.f」(ブラウザ表示用)
(注意:
個別ソースファイルへのリンクに関してはあくまでブラウザでの表示用です。右クリックでタブを開きファイルをダウンロード(「対象をファイルに保存」を選択)した場合、そのままではソースとしてコンパイルできません。リンクされるファイルは、ブラウザでの表示の都合上、ソースプログラム本体の前後にHTMLタグを付加し、さらに、PHPプログラムを使用してタグとしても使われるソース内の不等号記号( '<' , '>' )等を間接的な表示(文字実体参照)に加工されたものになっています。
これに関連して、通常表示のアドレスバーを見てわかるとおり、リンクされるサーバー内のファイルのファイル名の拡張子は「f」ではなく「php」に変更してあります。拡張子直前部分も「.f」を取り込んで「_f」などと変えてあります。ダウンロード後のファイル名の拡張子はさらに「php」から「htm」等に変わっています。)
中に2つのファイルがあると思いますが、それらが私が初めて出会ったFDTD法プログラムです。TeraPadエディタで開けます。プラズマの部分はとりあえず関係ない人がほとんどでしょうから、プラズマ密度=0として使用すれば良いです。どちらもFortran言語のプログラムで、「CompaqVisualFortran」という開発環境で動かすものです。ただし、これらに関しては私は実行はほとんどさせませんでした。2つのファイルの違いは解析する領域の外壁部分の扱いだけです。1番は外壁上に金属がない空間領域(外壁全部が吸収境界である領域)、2番は完全な導体に囲まれた領域を仮定しています。2番については、X座標が最小の面を電磁波の1次波源、✕座標が最大の面を金属なしの面として使っていたようです(この2面については完全な導体としての境界条件を設定する部分がコメントアウトされています)。(直前の1文を追加 2024.6.11) この後で私がいろいろ行ったのは1番 のタイプ です。(直前の1文を修正 2024.6.11)
続いて私が作ったファイルをお見せいたします。
解凍したフォルダー「FolderB」の中身
1. FORTRANファイル「FDTD2d-mur2-real.f90」(ブラウザ表示用)
2. C/C++ファイル「parabora-nameraka_20100730.cpp」(ブラウザ表示用)
3. Matlabファイル「AMPEZ_shori.m」(ブラウザ表示用)
5. PowerPointファイル「parabora.ppt」
(注意:個別ソースファイルへのリンクに関しては、FolderAのところで書いたとおりです。matlabファイル(拡張子mのファイル)についてはサーバ内ファイルのファイル名の拡張子を「php」ではなく「html」に変更してあります。どういうわけかPHP処理がうまくできなかったからです。目視で文字実体参照化不要を確認いたしました。)
今度は5つのファイルがあると思います。1番の「FDTD2d-mur2-real.f90」が「FDTD3dp01.f」と先に挙げた宇野先生の本をもとに私が作った2次元版FDTD法プログラムになります。これを動作させた時が最も驚きました。波元からマイクロ波ビームが伸びる様子がきれいに出ていました。
さらにこれをC++/C言語に書き換えたのが2番の「parabora-nameraka_20100730.cpp」になります。開発・実行環境はVisualC++2008です。昔のCompaqVisualFortanのものに比べると、配列サイズの制約がなくなっています(ヒープが使えます)(2021.3.10 削除)。これらのメインプログラムの補助をするのが3番の「AMPEZ_shori.m」です。これは吐き出されたテキストデータを可視化するプログラムです。ちょっと細かい説明になりますがAMPEZとはEZ(電界の紙面に垂直な成分)の振幅のことで、これの空間分布を表示しています(EZだけ見ていて大丈夫なのかというとソースの条件がこのモード用になっています)。動作環境であるMatlabが今手元にないのが痛いのですが、小さいデータならExcelでも表示できるはずです。
メイン計算の際には各空間位置の状態を誘電率なので表現してあげますが、それ以外にもいくつか重要な設定パラメータがあります。差分化パラメータです。それをどう決めるかを書いたのが4番の「DToptimize.xls」です。この中で1つだけ注意が必要なのはクーラント(Courant(2022.1.4 追加))パラメータ(この名前は私が考えたものですが例の本を見れば意味は分かると思います)で、これが1未満というのはきちんと計算するための必要条件で十分条件ではないということです。つまり、1未満でも振幅が発散する可能性すらあります。感覚的には0.5以下がいいです。その辺の理論はまだ私の中では十分になっていないです。どうもすみません。
最後の5番、「parabora.ppt」が大体どんな感じで使っていたかを示す文献になります。この文献の中での目的に対する結論はかなり怪しいです。どうもすみません。
お詫びと訂正
「FolderB」の「FDTD2d-mur2-real.f90」について
「gfortranで動かすと174行目付近にエラーがあるように出てくる」とのご指摘を受けました。以下のように直すと動いたそうです。
175,176行目を以下のように変更してください (こちらでは敢えてソースファイルそのものは直しませんでした)。 変更前 WRITE(6,'(a30,e10.5)')'全ステップ回数 =',ITMAX WRITE(1101,'(a30,e10.5)')'全ステップ回数 =',ITMAX 変更後 WRITE(6,'(a30,i5)')'全ステップ回数 =',ITMAX WRITE(1101,‘(a30,i5)’)‘全ステップ回数 =’,ITMAX
お詫びして訂正いたします。(2018.12.05)
この 項 節はやや長いので目次を付けておきます。
- 目次
- 3-1 6ノード2分割方式近傍点加算繰り返しアルゴリズム
- 3-2 Yeeアルゴリズムの追加説明
- 3-3 Yeeアルゴリズム(宇野先生の本のもの)を用いないFDTD法について
- 3-4 共通点と異なる点の整理
一通りプログラムの紹介が終わりましたので、ここでFDTD法のこれからについて私の考えを書きます。本当に実際にFDTD法は、教育、研究開発の現場などのどこかで使いこなせるのかという問題です。問題はいくつかあると思いますが、ここではYeeアルゴリズムの計算速度について考えてみます。大雑把な数字ですが、普通のPC1台で、3000×3000のYeeセルでステップ数5000ぐらいで2次元FDTD法計算を行うとたしか15分程度かかりました。FDTD法では1ステップ当たりの計算時間は総セル数に比例します。さらに、ビームが端から端まで届いて定常解に達するのに ビームが1次波源(例えば提出レポート「パラボラミラーによるミリ波ビーム絞り」の4ページ目図1では画像右下部分にあるホーンアンテナ(「ソース」となっている部分))から飛び出し始めた時刻から、ビームの先端がYeeアルゴリズム計算領域内の着目している領域(同提出レポート7ページ目図3では画像左上部分にある白い縦線線分上)まで完全に到達する時刻まで時間を進めるのに(「注1 計算上の注意点」も参照のこと) (2021.12.30、2022.1.3、2022.1.4 修正) 必要な総ステップ数は(計算領域が正方形、立方体だとして)1辺にならぶセルの数に比例します。そうすると、例えて言うなら計算結果が出るのに1時間かかる電卓のような感じになり、使う気が起こらなくなってしまいます。絵として(生データとしては「動画として」)(2021.12.30 追加) 見られる結果が出るような3次元FDTD法計算は現実的には困難ということになってしまいます。
そこで複数台のPCで協力して計算(並列処理)できないかという発想が出てきます。以下の図、fig.2 を見てください。並列処理の可能性を説明するために私が考えた簡易計算アルゴリズム「6ノード2分割方式近傍点加算繰り返しアルゴリズム」です。
注1 計算上の注意点(2022.1.4 修正)
最適ターン数の選択
時間的に振幅一定の1次正弦波波源から飛び出し始めたビームの先端に残る、定常振幅部分化した後のターン(の1周期分)でのその場所での振幅との違いである「ビーム先端爆発誤差」(この言葉は自分が勝手に作りました)は、はじめのターンの波源強度を適当に弱めることで大きさが減少した経緯があったはずです(このうまくいった場合には「ビーム立ち上がり過渡期誤差」の方がよい名前かもしれません)が正確なところは忘れました。初期波源強度の弱め方を研究したわけではありませんがとにかく宇野先生の本の通りにやることでこの誤差は定常振幅部分の振幅と同程度以下に収まり、この誤差がみられる部分の空間的な広がりは一連のシミュレーションでこれもうろ覚えですがいつもビームの進行方向において波長の2,3倍程度で収まっていたようです(上記の提出レポートでは使っていませんがFDTD法を過渡応答の解析に使う場合の数学的な議論は私にはわかりません。そうでない場合もですが...)。ですから、この誤差の部分が完全に着目領域を通り過ぎ終わるまで少しターン数は余裕をもって多めに計算しました。ただし、あまりターン数を多くしすぎると今度は吸収壁(レポートでは特に左辺)からの弱い反射波が解析の邪魔をするのでそこは丁度よいターン数を狙いました。ただし、大まかにカラーマップを見るだけならばそんなに目立つほどには反射波は強くはありませんでした。

fig.2
Yeeアルゴリズムと共通点のあるアルゴリズム
「6ノード2分割方式近傍点加算繰り返しアルゴリズム」
まず、直線上に等間隔にノードを並べます。図ではn1,n2,n3,n4,n5,n6と6個並んでいます。各ノードはある値を持っているとします。各ノードの値を以下のように計算してステップごとに変化させていきます。
n1 ← n1 + n1 + n2
n2 ← n1 + n2 + n3
n3 ← n2 + n3 + n4
n4 ← n3 + n4 + n5
n5 ← n4 + n5 + n6
n6 ← n5 + n6 + n6
たとえば一番上の式は 「第K+1ステップでのn1の値」 として 「第Kステップでのn1の値」 ×2 + 「第Kステップでのn1の値」 を採用することを表します。
n1とn6(FDTD法では外壁部分に相当)の計算の仕方は他と多少違いますが、基本的に自分と隣のノードの値だけを使って次のステップでの値を決めています。あるステップが完了するまで計算されたノードの計算前の値を保存さえしてあれば、同一ステップ内でどのノードの値を先に計算しても構いません。n1,n2, ... ,n6と順番に計算しても n2,n4,n6,n1,n3,n5 と計算しても最終結果に影響しません。このアルゴリズムはノード群を分割して、2つの別々に動くプログラムで協力して計算させれば、プログラム1つあたりの受け持つ計算量が減らせることは想像がつくと思います。つまり以下のようにします。以下の図、fig.3 を見てください。n3とn4の間に線を入れました。片方がn1~n3を、もう片方がn4~n6を計算するようにします。
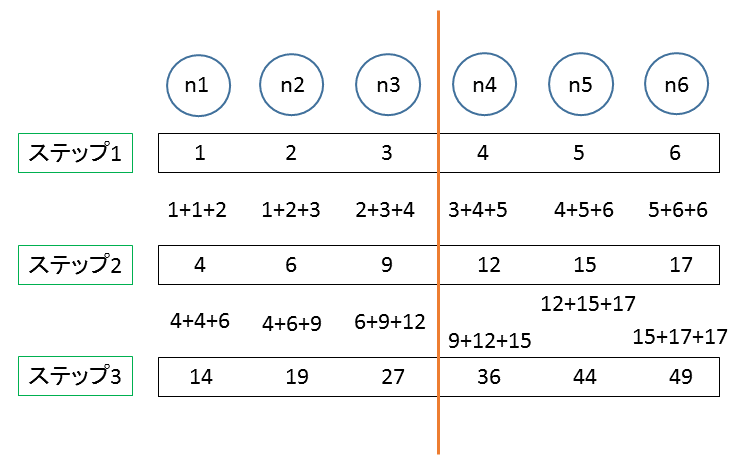
fig.3
計算量を2等分する試み
n1~n3を担当するプログラムを「プログラム1」、n4からn6を担当するプログラムを「プログラム2」としましょう。「プログラム1」だけに着目したのが以下の図、fig.4です。

fig.4
「プログラム1」の計算範囲+「プログラム2」側の分割境界近傍
n4が入っていることにお気づきでしょうか。そうです、「プログラム2」と通信をしてn4の値を持ってこなければn3の値は計算できません。といった感じで、多少通信処理による無駄が出るわけですが処理量を分担させるイメージはわかっていただけたかと思います。これが、FDTD法計算アルゴリズムにも基本的には当てはまります。
通信部分をどうやってプログラム化するかは、考えなければなりません。データ本体は小さくともパケットを用いた通信を行うなどすれば、ある程度の無駄な処理は避けられません。しかし、今回はあまり通信方法にこだわらずにとにかく「並列処理」するプログラムを作ってみたいと思います。と思いましたが、ある程度遊べる状態のものをと思ってまだできていません。
3-1 6ノード2分割方式近傍点加算繰り返しアルゴリズム-ここまで
「Yeeアルゴリズムを用いたFDTD法全体のアルゴリズム」および「6ノード2分割方式近傍点加算繰り返しアルゴリズム」の共通点と異なる点を整理したいと思います。 その前に「Yeeアルゴリズム」を少し細かく説明いたします。
次の図、fig.5は私が行っていた2次元FDTD法計算の場合のノードの位置を表しています。「2次元」というのは各物理量にZ方向依存性が無いと仮定した場合になります。計算にはX方向の磁場Hx、Y方向の磁場Hy、Z方向の電場Ezのみが登場します。電磁波伝搬モードの関係でHz,Ex,Eyは出てきません(先の本では「2次元TM_FDTD法」となっています)。各ノードに1つだけ求める物理量があります。fig.5でいうと、Hxはオレンジ色の下向きの矢印、Hyはオレンジ色の右向きの矢印、Ezは黒丸の入った青丸になっています(点線の枠内が先のfig.1でいうと縦の辺の中点の高さで横に切って上から眺めたものになります。XY平面内にすべてのノードを配置します)。なお、この図には外壁部分は入っていません(内部と大きな差はありません。ここでは領域分割による並列計算可能性の議論に必要な項目に集中したいと思います)。
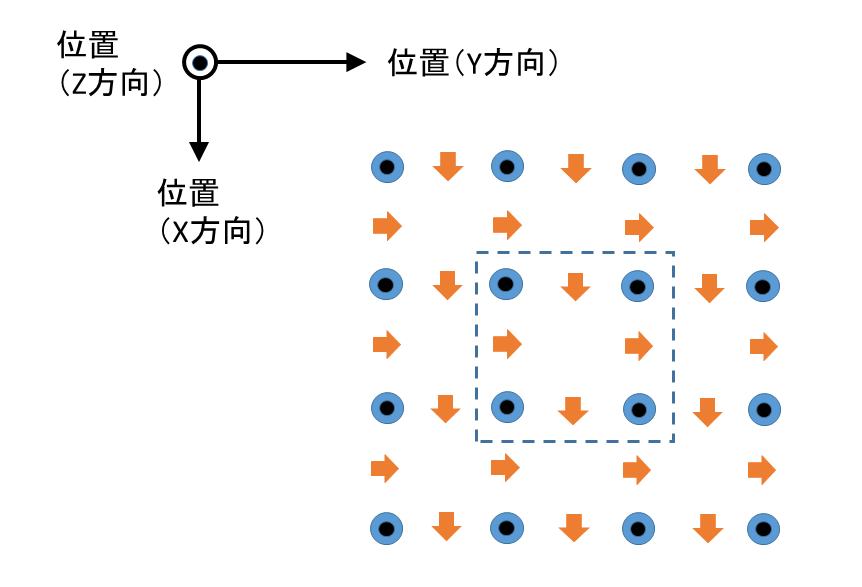
fig.5
2次元FDTD法(TM波)のノードの配置
そして、青の電場ノードとオレンジの磁場ノードをノードが持つ時間の時系列で交互に求めていきます。各時刻での計算内容、ノードの状態が上記の「6ノード2分割方式近傍点加算繰り返しアルゴリズム」の説明における各「ステップ」となります。青の電場ノードを計算するステップを「電場ステップ」、オレンジの磁場ノードを計算するステップを「磁場ステップ」とそれぞれ呼ぶことにします。電場ステップでは各電場ノードは1つ前の電場ステップ終了後での自分の値と直前の磁場ステップ終了後での上下左右の磁場ノードの値を、磁場ステップでは各磁場ノードは1つ前の磁場ステップ終了後での自分の値と直前の電場ステップ終了後での左右(下向き矢印の場合)、または上下(右向き矢印の場合)の電場ノードの値をそれぞれ用いて計算します(上記の本では電場、磁場の両ステップ1回分がまとまって1ステップとなっています)。
これをわかりやすく説明するために、無理やり1次元FDTD法というものを考えてYeeアルゴリズムのイメージを書くとfig.6~8のようになります。fig.6は電場が求まるノードを青い丸で、磁場が求まるノードをオレンジ色の三角で表したものです。横方向が「位置」になっています。これはfig.2のn1からn6までと同様です(ただし、fig.5と同様、fig.6でも外壁部分は入っていないものとします。だから正確に言うとfig.2の「n2」から「n5」までと同様です)。

fig.6
一次元にFDTD法のノードを並べる(?)イメージ
このノードは以下の図、fig.7のように計算が進みます。青い矢印があるノードを計算するのに必要なノードの値を表しています。fig.7では電場が求まっています。図中、縦方向に「時間」とあるのは計算対象(ノード)が持つ時間です。

fig.7
一次元FDTD法(?)の電場が求まっていくイメージ
そして、次の段階で磁場が求まります。この様子がfig.8で描かれています。

fig.8
一次元FDTD法(?)の磁場が求まっていくイメージ
ここまでで、大体わかっていただけたかと思いますが、上記の各ステップ(各横一列)で次のステップに行くための各ノードの計算において、使われているのは自分自身と隣のノードの値だけだということがわかります。ここが最大のポイントになります。「3-1 6ノード2分割方式近傍点加算繰り返しアルゴリズム」のところでもこの表現がありましたね。
3-2 Yeeアルゴリズムの追加説明-ここまで
ところで、以下の図、fig.9のように電場、磁場の1時間単位をセットにして計算する方法も、計算式をYeeアルゴリズムの差分式ではなく別のものにしておけばFDTD法としてあり得なくはないと思います。しかし、わざわざ時間軸で遠いノードを推定するのは誤差を大きくするだけでメリットはあまりないと思います。仮に、このアルゴリズムならばノードの計算順序は、電場、磁場を交互に行うといった必要はないことになります。

fig.9
一次元FDTD法(?)の電場と磁場が求まっていくYeeアルゴリズム(上記の本のもの)とは別のアルゴリズムのイメージ
3-3 Yeeアルゴリズム(宇野先生の本のもの)を用いないFDTD法について-ここまで
以上をもとに、「Yeeアルゴリズムを用いたFDTD法計算アルゴリズム」および「6ノード2分割方式近傍点加算繰り返しアルゴリズム」の共通点と異なる点を整理します。
共通点1
「空間分割(ノード分割)により並列処理ができる(処理量の分散が容易である)」
共通点2
「複数ステップ分の通信を1回で行うことができる」
電場ノード、磁場ノードは別のステップで計算するということでしたが、電場ノード計算の前、磁場ノード計算の前に別々に通信する必要は必ずしもありません。例えば境界付近の電場ノード1層、磁場ノード1層の計2層のデータを相手側に渡しておけば、2ステップ分の通信は1回で済みます。3層分渡せば3ステップが1回にまとまります。
異なる点1
「FDTD法アルゴリズムでは、電場と磁場の2種類のノードがある、そしてさらにYeeアルゴリズムでは電場、磁場が交互に求まる」
異なる点2
「波源の有無」
ところで、FDTD法では金属部分や電磁波源があることが普通です。これらも含めると、例として以下のように書けます。波源部分では計算式に隣接するノードは 出てきません。この意味で金属部分も一種の波源と言えます。波源部分でも、「各ステップで次のステップに行くための各ノードの計算において、使われているのは自分自身と近いところのノードの値だけ」がより厳しく満たされているので「共通点1」に影響はありません。
nn1 ← nn1 + nn1 + nn2 (外壁部分に相当)
nn2 ← nn1 + nn2 + nn3
nn3 ← 0 (金属部分に相当)
nn4 ← nn3 + nn4 + nn5
nn5 ← nn4 + nn5 + nn6
nn6 ← nn5 + nn6 + nn7
nn7 ← (ステップ数)×(ステップ間隔)×2 (電磁波源に相当)
nn8 ← (ステップ数)×(ステップ間隔)×3 (電磁波源に相当)
nn9 ← nn8 + nn9 + nn10
nn10 ← nn9 + nn10 + nn10 (外壁部分に相当)
異なる点3
「各ノードの初期値 」
波源、金属以外の部分では私がやっていたシミュレーションでは初期値が0でした。そこは「6ノード2分割方式近傍点加算繰り返しアルゴリズム」の議論のときと違っています。
3-4 共通点と異なる点の整理-ここまで
最後に、FDTD法計算の高速化を図るうえで上記の並列化がなぜそんなに有望な選択肢なのかということについて私の考えを書いておきます。
- ソフトウェア
- 並列処理をする・しない
これについては、仮に並列化可能なハードウェアをもっているのなら(この前提の評価が難しいのですが、速度の問題だけならそんなに計算主体同士の結合度は要らないようです。力任せにパソコンを買いそろえてつないでもできるでしょう。環境負荷を考えてもっと小さく軽くと言い出すとハードルは上がりますが)、「プログラムがややこしくなるから」程度の理由でやらないという手はないでしょう。
並列化可能なハードウェアの構成は後で書くようにあります(Web技術そのものです)。処理方法(アルゴリズム)も「3-1 6ノード2分割方式近傍点加算繰り返しアルゴリズム」で書いたように具体的にあります。ただし、処理速度において意味のある並列化になるかは、また別の話であり、考えたくありませんが、必要となる計算主体同士の結合度があまりにも高い場合、「プログラムがややこしくなるから」の理由で不可能になる可能性も否定できません。そうではなく、「純粋にハードウェア的に無理」という可能性もあります。後者については、後で(「4-2 並列化後の速度面の最低保証について」の中で)、可能な限り考察します。あと、私がうまく紹介できないだけで、本まで出して並列化したFDTD法を行なっている先生もいらっしゃるようです。(2023.5.15 訂正) - 並列処理をする場合の通信パラメータの最適化
たとえば相手の計算進捗状況を頻繁に確認しすぎて自分がへとへとになってしまっても困ります。その確認頻度ぐらいは少なくとも専用ハード成熟期前の初期段階ではソフトウェアで変更可能となっているべきでしょう。他には相手から1度に読み込むデータ量などが思いつきます。
たとえば通信相手(自分とは異なる動作クロックで動いている計算主体)の計算進捗状況を頻繁に確認しすぎて自分がへとへとになってしまっても困ります。通信パラメータとして「通信相手の状況確認の頻度」は最適化されるべきでしょう。他には「相手から1度に読み込むデータ量」などが思いつきます。ただし、最終段階(成熟した専用ハードウェア上)でも、FDTD法計算の種類、目的によって通信パラメータの理想値最適値は異なるかもしれません。その前段階なら「ハードウェア開発のために」という理由も加わり、さらにソフトウェアで変更可能としておくことが重要になるような気はします。ただし、必要以上にソフトウェアを充実させようとして、同じ性能を出すためのハードウェアが変わってしまったり、理想値最適値が変わってしまったり、性能が落ちてしまったりしては本末転倒でしょう。この匙加減までは私にはわかりません。よくできたOSでパラメータが用意されているのなら、「まずはおとなしくそれを使う」ということでよいような気はします。(2023.4.2 訂正、2023.4.15 言葉の変更) - その他
セキュリティチェックは外しておきたいものです。
- ハードウェア
- CPU内部
トランジスタの内部なら、使用する物質の性質が重要です。この部分の話は古典的な電磁気学(このサイトのテーマであるFDTD法で原理的には解けるはず)の話以外にミクロスケールの話(量子力学)が出てきます。信号伝達時間はキャリア(電子、正孔)の移動速度が効いてきます。私にはよくわかりませんでしたが、半導体工学の勉強の中で出てきました。トランジスタの外部の話なら、マルチコアプロセッサが最近よく聞くワードです。非常に多くのトランジスタ間、トランジスタとメモリー間の配線引き回しが重要になります。信号伝達時間は古典的な電磁気学で見積れるはずです。配線の寄生容量とかよく聞きます。各素子の微細化はまだいくらかは続くようです。
- CPU外部のPC内
配線引き回しが重要になります。信号伝達時間は古典的な電磁気学で見積れるはずです。
- PC外
配線引き回しが重要になります。信号伝達時間は古典的な電磁気学で見積れるはずです。
ただし、PCの台数が増えてくればルーター、ハブ等の中継機器も重要でしょう。ただし、PCの台数が増えてくれば、ルーターも重要でしょう。関係ないデータのパケットの処理を多くのPCに強いるべきではありませんからカットすべきものはさっさとカットしたいです。計算機資源の無駄ですし、速度面でも、ルーターが2つ(送信側と受信側)間に挟まることによるマイナス効果より、受信側PCがたくさんの要らないパケットを無視しなければならなくなるマイナス効果の方が絶対に大きいと思います。一応根拠を書きます。単純に考えられるように、PC1台1台にそれぞれルーターをつないだ場合で考えます。ルーターは1台につき、自分のPCから2次元計算なら隣接空間領域を担当する最大4台(3次元計算なら最大で6台)のPCに向かうデータとその4台からルーターを通してくる自分のPC宛のデータだけ担当すればよいので、必要な処理量(パケット解析数)にはそんなに大きくならないはっきりとした上限があります。不要なパケットのカットは特別に意識しなくても出来ていることになります。あるいは、インターネット通信(TCP・UDP/IPプロトコルによる通信)にこだわらず、通信速度の物理的限界値に少しでも近づけるということでいえば、後にも書きましたが汎用PCを諦めてルーターが要らない専用のユニットを用意するべきでしょう後にも書きましたがルーター無しで直接たがいにつなげられるユニットを用意するべきでしょう。(2022.11.22 訂正、「後にも書きましたが~」を2023.5.4 訂正)
いろいろ書きましたが、私個人が感じていることは、モノ作りの現実的な改善速度が急激に低下するレベルまでハードウェア的にはどの部分も来てしまっているということです。この並列化を除いては、です。上記の「キャリアの移動速度」(専門的には「キャリアの移動度」)は、量子力学で説明されるものではありますが、特に極微細構造を作らないと測定できないというようなものではありません。私も大学院生の時にファン・デア・パウ法で測定していました。化合物半導体膜上のパターンでも理論値と比較してそこそこの値でした。だから、出回っているCPU内の半導体の電子物性値としてはおそらく完全単結晶ウエハの理論値通りでしょう。そうなると、動作速度向上のためには配線の工夫以外には、ただひたすら素子の微細化をしていくしかないということになり、これまでさんざんやられてきたことになります。しかし、これからは、原子の粒が数えられるぐらいのサイズの構造物ということで、良い意味でも悪い意味でも動作の際の理論的に新しい量子力学的な効果を考えなければならないということはとりあえず脇に置いておくにしても、作りにくさは半端ではなくなるということです。それでも、量子コンピュータとしてよく語られているぐらいの速度が得られるならやるべきかもしれませんが、とにかく構造物を実際に作ることが難しいと思います(量子コンピュータに極微細加工が絶対に必要かについては私はよく知りません)。
そういうわけで、「上記の並列化のアイデアによって、基本素子の今以上の微細化に頼らなくても、速度面で電磁気学の勉強に使えるコンピュータを作ることはできるはず」と言いたいわけです
(ここでいう「基本素子」とは、CPU内の単体トランジスタや1ビット分の電荷を収納するメモリー領域 レジスタ領域(2022.11.21修正)や、金属、金属のような性質を持つように不純物を高ドーピングされた半導体でできている最小設計幅の配線部分などのことです)
(ここでいう「基本素子」とは、ウエハ表面に作られたCPU内の各パーツで具体的には単体トランジスタや、金属、金属のような性質を持つように不純物を高ドーピングされた半導体でできている最小設計幅の配線部分などのことです(2023.4.27 訂正))。ただし、その場合でも本当の限界性能は自分も含めて多くの人にとって作ってみないとわからないことがいろいろあると思います。「よし、とりあえず荒っぽくでも作ろう!」となるモチベーションとしての速度面での最低保証の方は例えば上記のプログラムを実際に動かしてみれば感覚としては納得していただけるのではないでしょうか。
とりあえず、「よし、とりあえず並列化したハードウェア・ソフトウェア一式を荒っぽくでも作ろう!」となるモチベーションとして、並列化前の速度面での最低保証の方は例えば上記のプログラムを実際に動かしてみれば感覚としては納得していただけるのではないでしょうか。(2023.5.15 訂正)
(2023.5.15 題名を「速度面の最低保証について」から変更)
並列化後の速度面の最低保証について私にできる限りの話を具体的に書くと次のようになります。FDTD法2次元計算で例えば3000セルx3000セル、5000ターンで 所要時間15分 = 900秒 なら1秒で5ターンちょっとなので、もう少し大きいサイズで10000セルx10000セルなら1ターンの計算につき1秒は超えます(記憶では実際にそんな感じでした)。理屈がわかりやすいように敢えて正確に計算していきます。まず、このPCの計算能力は
3000x3000x5000/900 = 5x107 (2次元)
5x107x3/6 = 2.5x107 (3次元)
セル・ターン/秒ということになります(本当は吸収境界壁等の計算が重いのでもっと大きい値かもしれませんが(作ろうとしているものは逆にこういう部分に引っ張られて小さい値かもしれませんが担当セル数に差をつける等、回避策はあると思うので)無視します)。ここで、3次元の方は1セル当たりのノード数を考慮して値が下げられています。(上記の2次元プログラムではEZ、HX、HYの3つ、3次元プログラムではEX、EY、EZ、HX、HY、HZの6つがノード数になります)。3次元では1つのノードを求める式も、ノードによって(今回の場合HXとHYが)やや長くなるようです(勉強不足と忘却が入っています)がここでは無視しました。以降の議論では、丁度1ターン1秒となるように1台のPCが受け持つセル数を
5x107 (2次元)
2.5x107 (3次元)
にそれぞれ固定します(1ターン1秒は遅い!という方がほとんどでしょうがとりあえずこうします)。この場合、1辺のセル数は正方形領域の2次元計算、立方体領域の3次元計算それぞれで
(5x107)0.5 ≒ 7071 (2次元)
(2.5x107)0.333 ≒ 291 (3次元)
セルとなります。1ターン当たり発生する通信が必要なデータ量は以下のようになります。隣接PCだけに渡すもののみ送信すればよいので、1台のPC(と1台のルータのセット)当たりで
- 2次元の場合
1辺7071セル x 最大4辺の隣接PC x 1セル当たりのノード数3(3つの倍精度浮動小数点型データが発生する)x 倍精度浮動小数点型のビット数
= 7071x4x3x64
≒ 5.4x106 - 3次元の場合
1面2912 セル x 最大6面の隣接PC x 1セル当たりのノード数6 x 倍精度浮動小数点型のビット数
= 2912x6x6x64
≒ 2.0x108
ビットとなります。もっと1台当たりのセルを減らす場合、例えば1辺のセル数を半分にすると2次元なら、1ターン当たりの所要時間は4分の1、1ターン当たりの通信量では半分で、両方の効果により時間当たりでは2倍になります。3次元ならそれぞれ8分の1、4分の1でやはり2倍になります。それでも、昨今のインターネット通信での伝送速度はかなり大きい値だと思います(ある有名な通信会社も「10ギガ(=1010)ビット毎秒」のコースを既に出しています)。
それで、ソフトウェアとハードウェアと両方の勉強を適当な割合で行なうことに意味があると考えます。
(「いろいろ書きましたが~」の部分を 2022.3.21 に修正、「そういうわけで~」以降を 2022.10.6、2022.10.24、2022.10.26 に修正、追加)
補足
「1ターン当たり発生する通信が必要なデータ量」について
上記の値は送信データのみの場合で、実際には送信と受信が必要であり、2倍になります。
「ある有名な通信会社も~」の記述について
上記の値10ギガビット毎秒という値は動画配信等も意識されているはずで、UDPプロトコルによる速度重視型の通信とTCPプロトコルによる信頼性重視型の通信では速度は異なるはずです。必要なハードウェアについては、本気では尋ねなかったのですが、たまたまインターネット通信のコース変更の際に、コールセンターの人がちょこっと言っていたことによると「高めのPCがあればこの高速のコース(正確にはプラン)を使う意味がある」というような感じでした。どうでもいいですが、私は実質無料のもっと低速のコースを選びました。ルーターだけは最近買い換えました。(2023.4.15 「必要なハードウェアについては~」の部分を追加)
その他の補足
上記の「速度面での最低保証」を元にハードを組んだら、次は並列処理専用の信号線を用いてお互いをルーター無しで直接つなげる専用ユニット(イメージとしては、専用ポートが4個か6個(送信、受信でも分けるなら8個か12個)付いているもの)を汎用PCの代わりに作れば、パケットの作成、解析の手間が省け、速度はアップすると思われます。それでも、CPUのクロックレベルで全システムを同期させたものを作ろうとするよりは敷居は低いでしょう。作るのに必要な知識は増えそうですが、それでも、「ターン終了ごとにCPU同士を同期させる」という考え方を用いずに、システム全体の動作クロックとして1種類かつ1つだけを用いようとするよりは敷居は低いと思います(PC(ラズベリーパイ)と周辺機器との通信を勉強すると比較的遅い2次的なクロックがCPUで生成されるという話が出てきました...)。(2023.3.24 修正)
まず、PCとルーターを用いてハードウェアを組むのがよいと思います(今の私はこれだけでもソースプログラムの提供もできず苦労していますが...)。ただし、この段階で全体のパフォーマンスとして「10ギガビット毎秒の通信」が活かされている状態が得られるかは保証できません。例えば、重いファイルのやり取り等で長い時間の間に1回だけ大きなデータを送信または受信するのと、このFDTD法並列計算での通信機能の使い方はかなり異なっています(後者では1回当たり比較的小さめのデータ量を計算への使用を挟みながら頻繁にやり取りします。無視できないほどのオーバーヘッドが生じる可能性は十分にあります)。
次の段階で、(単なるルーター内臓型ではなく)通信プロトコルを変更して、並列処理専用の信号線を用いてお互いをルーター無しで直接つなげる専用ユニット(イメージとしては、専用ポートが4個(2次元)か6個(3次元)(送信、受信でも分けるなら、さらに増えて8個か12個)付いているもの)を普通のPCとルーターのセットの代わりに使うようにします。すると、パケットの作成、解析の手間が省け、プロトコル次第では装置は簡略化が見込めます。ここまでやるとなると、作るのに必要な知識は増えそうですが、それでも、「ターン終了ごとに(あるいは1ターンにつき節目の数回だけ)CPU同士を同期させる」という考え方を用いずに、システム全体の動作クロックとして1種類かつ1つだけを用いようとするよりは敷居は低いと思います(PC(ラズベリーパイ)と周辺機器との通信を勉強すると比較的遅い2次的なクロックがCPUで生成されるという話が出てきました...)。で、この場合に上記のオーバーヘッドは消えそうなのかというとごめんなさい、わかりません。「並列化後の速度面の最低保証」は今回は失敗です。(2023.5.4 訂正、2023.5.15 最後の文に「並列化後の」を追加)
訂正
「[1倍精度浮動小数点数を表すビット数]」を「倍精度浮動小数点型のビット数」に訂正
(補足・その他の補足・訂正の部分を2022.11.21に追加)
(この項を2025.1.26に追加)
すぐ上の「その他の補足」の中で「ターン終了ごとに(あるいは1ターンにつき節目の数回だけ)CPU同士を同期させる」という考え方が有効だと述べましたがこの考え方を少しだけはっきりさせておこうと思います。以下に図を並べました。「ターン終了ごとに1回だけCPU同士を同期させる」場合の例になります。この方法だと同期のための信号を送るだけの司令塔PCは要らないのでまさにWebシステムそのものか類似のものになると思います。
全11枚
最後に、参考にした文献を挙げておきます。ここに挙げた以外にも、たくさんの本等を参考にしました。著者らには感謝申し上げます。最後の文献については指導教官であった 筒井 一生 先生に感謝申し上げます。
<C言語、C++言語について>
「プログラムを作ろう!MicrosoftVisualC++2008ExpressEdition入門」Wingsプロジェクト 著 出版社:日経BPソフトプレス
「14歳からはじめるC言語わくわくゲームプログラミング教室」大槻 有一郎 著 出版社:ラトルズ
<FDTD法について>
「FDTD法による電磁界およびアンテナ解析」宇野 亨 著 出版社:コロナ社
<「キャリアの移動度」の測定について>
東京工業大学大学院修士論文
「GaAs/CaF2表面改質エピタキシーにおける電子線照射条件に関する研究」 駒田 寛
Copyright (c) 駒田 寛 のサイト All Rights Reserved.